פרק ה: מידת הדיוק של שיעורי חכמים וסיבתה

1. הבעיה בכללים ההנדסיים של חכמינו

שני כללים עיקריים נתנו חז"ל בחישובים גיאומטריים (מלבד כמה שיעורים אחרים, כמו כלליהם של דייני דקיסרי [פרק ב] או בכללים הנובעים בדרך עקיפין ממדות שנתנו, למשל בענייני עמוד חלול (פרק ח סעיף 2

ובלתי חלול ( המוטל לאורכו על הארץ).

האחד בחישובי עיגול - שטחו והיקפו, והשני, בדבר אלכסון ריבוע שצלעו יחידה , השווה בערכו ל 2√, ביחס לעיגול אמרו שני דברים שמשמעותם אחת:

ש"המרובע יתר על העיגול רביע" ( אהלות פרק י"ב משנה ו) כלומר, שהעיגול החסום בתוך ריבוע שווה, בין בשטחו ובין בהיקפו ל 3/4 מהריבוע( ראה לעיל פרק ) וכן, ש"כל שיש בהיקפו שלשה טפחים יש בו רוחב טפח" (מסכת עירובין, פרק א משנה ה)

פירושם של שני הכללים הללו הוא: π=3 ומימלא, זה קובע שהיקף העיגול גדול פי 3 מהקוטר ,

 וכן ששטחו הוא 3/4 משטח הריבוע החוסמו 

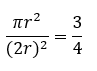
על 2√ אמרו רבותינו:

"כל אמתא בריבועא - אמתא ותרי חומשי באלכסונא" (עירובין נ"ז ע"א; ע"ו ע"ב, סוכה ח ע"ב ועוד) שפירושו הוא 2√=7/5

בקירובים אלו ואחרים, דנו הראשונים והאחרונים, ורובם ככולם נגעו בשאלה, עד כמה יש לדייק בשיעורים האלה, שהרי לעולם אי-אפשר להגיע לשיעור האמיתי, שכן מספרים אלה אינם רציונליים. האם יש לדייק יותר מהשיעור שנתנו חכמים, או לא, ואם-כן - מדוע לא החמירו חכמים בשיעוריהם כדין "לא-דק" שבתלמוד, ושמא לא הקלו אלא בדברים שהם מדרבנן, מעין "הם אמרו והם אמרו".

בכל אלה דשו המפרשים והפוסקים וכמה שיטות ביניהם.

התשב"ץ (כרך א, חלקים א-ב) דן בשאלה זו באריכות והביא את הדעות השונות. האחרונים שבאו אחריו עסקו בהן אף הם ופיתחו אותן.

2.     דעת המאירי: לא דקו רבנן

לפירושו של המאירי בדברי דייני דקיסרי (עירובין ע"ו ע"ב; סוכה ח ע"ב) " עיגולא מיגו ריבועא-ריבעא, ריבועא מיגו עיגולא- פלגא"  דברו הם ביחס לשטחי צורות גיאומטריות אלו ודבריהם נכונים לפי כללי הש"ס - אלא, שאף על פי כן, לא נמנעה הגמרא מלומר על דבריהם:

"ולא היא דהא קחזינן דלא הוי כולי האי"

כיון ש π, אליבא דאמת, גדול מ 3. נשאלת א"כ מיד השאלה מדוע לא אמרה הגמרא בכל מקום שסמכו על הכלל π=3 , "ולא היא" ולא חיפשה תמיד ערך קרוב יותר. בתשובה לשאלה זו אומר המאירי:

"ואף על פי שאף לשאר החכמים היה יכול לומר "ולא היא" שהרי על דרך האמת יש להקיף העיגול על רוחב הקוטר שלוש כמותו ועוד שביעית רוחב הקוטר, עד שאם רוחב הקוטר שבעה יהיה ההיקף כ"ב וכן שכל אמתא בריבועא הוא יותר מאמתא ותרין חומשי באלכסונא, מכל מקום , לענין מדידה - אין הכיוון מצוי בו כל כך עד שנדקדק עליהם בדבר מועט, אבל דייני דקיסרי שהיו מדברים על דרך התשבורת ושהיו סבורים להעלות דבריהם בדקדוק מכוון, היה ראוי לדקדק עליהם ולהודיע שאף הם עם כל הפלפולים - לא כוונו את הדבר לצמצם לגמרי"

כלומר בד"כ , למעשה לא מתעוררת הבעיה כי "אין הכיוון מצוי". ורק כשיש לנו עניין בדיון מתמטי טהור, טורחת הגמרא להעיר שהכללים - π=3 ו 2√=7/5 אינם מדוייקים.

ובאותו עניין עצמו, דין חלון שבין שתי חצרות, שהגמרא מסיקה ביחס אליו "בשיבסר נכי חומשי סגיא" , עפ"י קירוביה, מצא המאירי לנחוץ לומר שאין לסמוך על שיעור הגמרא שנאמר בדרך הקירוב, "אלא שכתבו גדולי המפרשים, אף לדעת זה, (כלומר למסקנה) ר"ל, על היקף שיבסר נכי חומשא שלא יצמצם אדם במידה זו, מפני שחכמי המידות כתבו שכל אמתא בריבועא הוא יותר מאמתא ותרין חומשין באלכסונא, וכן כל שיש בו רוחב טפח יש בו יותר משלשה טפחים היקף. ועל דרך האמת כל עיגול שיש ברוחבו איזה שיעור יהיה בהיקפו שלוש כמותו ועוד שביעית וגם זה בקירוב כי לא יודע בצמצום גמור לפי מה שכתבו החכמים, ולחשבון זה יבוא למבוקש (ר"ל , לדין חלון עגול) יותר משבעה עשר" (ולמעשה, יש לדקדק, ולהתיר רק חלון שיש בו יותר מהחשבון האמיתי שהוא גדול מ 17)

התשב"ץ בהביאו שיטה זו, הסכים איתה, וגם הוסיף עליה ביאור להסביר מדוע בכל "לא-דק" שבתלמוד מקפידה הגמרא לומר: אימור דאמרינן לא-דק לחומרא, לקולא מי אמרינן?

וכאן בעניינינו, פעמים הרבה יש קולא בדבר ויוכל לבוא לידי קלקול, ומימלא, לא יספיק רק מה "שאין הכיוון מצוי":

בראשית דבריו באר מה שכל המפרשים מודים בו, שלא מחמת חוסר ידיעה אמרו מה שאמרו, שהרי אפשר למדוד בנקל ולמצוא ששיעורים אלה אינם מדויקים. עוד כתב שם:

"שלא נעלם מהם האמת, כי הם אנשי האמת, מקבלי האמת מא-הי האמת"

אף הוא הזכיר שם מקום אחד שבו הראו חז"ל במפורש שהם ידעו כי אמתא ותרי חומשי אינו שיעור מדוייק ובדין גינה וקרקף (עירובין פרק ב משנה ה) נתנו את השיעור : 2√*50=702/3

בעוד שלפי {} די היה ב 70 (פרק ד סעיף 1)

בהמשך דבריו הביא את השיטות העיקריות לפרש את הדברים והסכים עם השיטה הנ"ל:

"שנאמר שהם כשנשאו ונתנו בזה העיקרים אלו עשו זה לקרב ההבנה אל התלמידים, לפי שלעולם ישנה אדם לתלמידו בדרך קצרה.."

כוונתו לומר שאע"פ שבד"כ יש לדייק ואם לא מדייקים - יש להחמיר, הרי כאן שזה עניין שהתלמידים עלולים להתבלבל בו אם ידקדקו בשיעורו, כאן יכול חכמים שלא לדקדק והלכו לפי כלליהם אפילו לקולא, "אבל לענין ע"פ הדקדוק האמיתי, ומסרוהו (כלומר, חז"ל השאירו את החישוב המדוקדק) לחכמים יודעי השיעורים, נמצא כי ההלכה מסורה לתלמידים המתחילים והמעשה מסור אל החכמים לדקדקו על פי האמת. וזה הדרך ישר בעיני לתיקון דבריהם ז"ל"

סיוע לשיטה זו רצה התשב"ץ להביא מעמוד המוטל באויר (אהלות י"ב משנה ז) שחכמים לא דקדקו בו אפילו לפי כלליהם אע"פ שלפי הפירוש הרגיל די היה ב 21 טפחים והם נתנו שיעור של 24. הסיבה לכך היא שהתנא לא רצה לייגע את הלומד בחישובים ארוכים וקירב את החשבון. ולמעשה יש לתת לעמוד דין אוהל מהשיעור האמיתי ואילך (בערך 22 טפחים).

אפשר לחשב גם את הרמב"ם כאחד מבעלי שיטה זו, אע"פ שבכמה מקומות הביא את שיעורי הש"ס, מכל מקום, שייר גם הוא, למעשה, מקום להחמיר ולהקל לפי הדקדוק האמיתי. וכך כתב בענין קורה עגולה של מבוי.

"וכיון שזה לא יושג לגמרי, אלא בקירוב, תפשו הם בחשבון גדול ( כלומר שיערו מידותיהם בקירוב, ובאמות או בטפחים שלמים) ואמרו שכל שיש בהיקפו ג' טפחים יש בו רוחב טפח והסתפקו בזה בכל המדידות שהוצרכו להן בכל התורה."

משמע מכאן שמתוך שקשה להשיג את החשבון ואי אפשר לדקדק בו כראוי, הסתפקו חכמים בחשבון מקורב, על אף שלמעשה יש להקפיד על השיעור האמיתי.

לכן קשה לייחס לרמב"ם פירוש שהובא בשמו לעניין כוורת ( חידושי הרמב"ם לתלמוד ע"ב ) שחכמים החמירו לפי הדקדוק האמיתי ונתנו לאלכסון ריבוע שצלעו 4 טפחים למעלה מ 5 טפחים ו 3/5 הטפח, שהיה די בהם לפי כלליהם, שהרי כאן פירש הרמב"ם שלדעתו לא סטו חז"ל בשום מקום מכלליהם.

3. הדעה השנייה: "הלכה למשה מסיני"

דעה שניה על השיעורים הללו הובאה בקצת הראשונים והרבה אחרונים החזיקו בה. לדעה זו, השיעורים π=3 ו 2√=7/5 הם שיעורים שנתנו למשה בסיני, כך יש לנהוג למעשה  ואין לדייק בחשבון, מכיון שככל שתקרב לא תגיע לאמת. חלק מבעלי דעה זו אמרוה רק ביחס לכלל π=3 ויש מהם שאמרוה על שני הכללים.

סיוע לדבריהם מצאו בדברי הגמרא על הכלל "כל שיש בהיקפו שלשה טפחים - יש בו רוחב טפח". על כלל זה שאלה הגמרא: " מנא הני מילי?" - ופישטה:

"אמר ר' יוחנן: דאמר קרא: [מלכים א פרק ז פסוק כ"ג]: ויעש את הים מוצק עשר באמה משפתו עד שפתו וקו שלושים באמה יסוב אותו סביב"

אילו היה זה עניין של מדידה לא היה עלינו ללמוד את הדברים מן הפסוקים אלא למדוד בעצמינו.

התשב"ץ (בעניין הנ"ל) הביא בענין זה את לשון התוספות (שאינם לפנינו):

"תימה, מה שייך למיבעי, מנא הני מילי, בדבר שאדם יכול לעמוד עליו? יביאו דבר שהוא רחב טפח ונמדוד ההיקף. ונראה שלפי זה שאין הדבר מכוון, דטפי ודאי הוא, משום הכי קא בעי: מנא לן מקרא דלא דייקא בההוא פורתא דהוי טפי? ומייתי ראיה מים שעשה שלמה שהוא רחב עשר אמות וקאמר דקו שלושים באמה יסוב אותו , ואף על גב דהוי טפי פורתא , קרא לא דייק בהכי - מהתם ילפינן רבנן דלא למידק"

התשב"ץ באר שיטה זו והסבירה על אף שלבסוף דחאה:

"או שקבלתן היתה ללכת על פי דרכים אלו, ואע"פ שיש בהם קירוב דהא שיעורין - הלכה למשה מסיני הם, כדאיתא בעירובין ובסוכה ובדוכתי אחריתי, ואפשר לומר שכך נאמרה ההלכה, כמו שאמרו בקידושין על ענין אחר, והטעם בזה, לפי שלא ניתנה התורה למלאכי השרת כמו שאמרו בברכות וקידושין על עניינים אחרים, ושמא כך נמסרה להם הלכה שיתנהגו על עיקרים אלו אע"פ שיש בהם קירוב, כאילו הם מדוקדקים ויש סמך בזה מים שעשה שלמה שהלך בו הכתוב על דרך קירוב כמו שביארתי"

כמה מהאחרונים כוונו לדברים האלה. לדוגמא, אביא את דברי בעל "תפארת-ישראל" (על עירובין פרק א משנה ה) על המשנה הזאת כתב הוא בעניין זה:

"...על פי מה שכתב הרמב"ם שמה שאמרו חז"ל דכל שיש ברחבו טפח, צריך להיקפו ג' טפחים, ואינו בדקדוק, דבאמת, צריך להיקפו ג' טפחים ושביעית בקירוב. (ובזה נראה לי לישב מה דאמרינן (עירובין י"ד) מנא הני מילי דכשיש ברחבו טפח, יש בהיקפו ג' טפחים, ויליף לה מים שעשה שלמה. וקשה: למה לי קרא, והרי דבר הנראה לעינים הוא? אלא הש"ס הכי קא קשיא ליה: מנא לן דאע"ג שהוא קצת יותר חשבינן לה כך"

 ב"תפארת -צבי" ( ר' צדוק בן יעקב הכהן מלובלין, על שולחן ערוך יורה-דעה) כתב על דברי התשב"ץ:

"ואע"פ שבדרך הב' אמר שלמעשה אינו כן (כלומר כשיטה הראשונה, שלמעשה יש לנהוג לפי החשבון האמיתי) ודאי שלא אמר זה אלא להפיס דעתו של אותו חכם המהנדס והמתפלסף. (כוונתו לאנבלשום אפרים, שאת דבריו כתב התשב"ץ תוך כדי החלפת מכתבים איתו בעניינים שבתלמוד) אבל לקושטא, העיקר כדרך הראשון, כי איך סלקא דעתך להיות כל דברי המשנה והתלמוד הבאים להורות המעשה אשר יעשון כדי שלא ישתכח תורה, יהיה דבריהם להלכה ולא למעשה ותפוג תורה ללמוד על מנת לעשות, ואיך ישימו מכשול, אולי מי יורה מתוך דבריהם לעשות?!

אלא ודאי קושטא קאי דהעיקר כדרך הראשון שכתב, כי רז"ל כך היתה קבלה בידם לסמוך אכללא דכל שיש בהיקפו וכו', אע"פ שאינו אלא על צד הקירוב ואפילו להקל" (עוד אחרונים הלכו לפי שיטה זו)

4.  דרכים אחרות שנדחו

אנבשלום אפרים כתב לתשב"ץ, כפי שמשתמע מהתשובה שהשיב לו התשב"ץ, שחכמים לא דייקו בחשבונותיהם ויש לתת לדברים דין של לא-דק רגיל שעליו נוהגת הגמרא לומר ( סוכה ח ע"ב; בבא-בתרא כ"ז ע"א ועוד הרבה) "אימור דאמרינן לא-דק- לחומרא, לקולא מי אמרינן?"

הוא הוסיף שחכמים סמכו על כלליהם רק לחומרא, כגון במה שנתנו שיעור של 702/3 ל 2√*50 בעניין שיעור בית סאתיים (שולחן ערוך, יורה דעה, פרק ב. דף כ"ג ע"א) אעפ"י שהוא מעט יותר מזה. ע"י מה ששיערו הם - החמירו להקטין את השטח שיכולים לבוא בו קולות רשות היחיד כשיוקף (ואף לפני חשבון "אמתא ותרי חומשי", די היה ב 70 אמה , מכל מקום כיון שהשטח גדול - דייקו יותר.)

התשב"ץ דחה את האפשרות הזאת בפשטות מתוך דברי המשנה על קורת מבוי שצריכה עובי של טפח (עירובין פרק א משנה ה) עגולה- רואין אותה כאילו היא מרובעת, כל שיש בהיקפו שלושה טפחים יש בו רוחב טפח" כלומר, די בהיקף של שלושה טפחים כדי להכשיר את הקורה, ולפי הדיוק המתמטי אין בקוטרה טפח והיתה צריכה להיפסל למבוי.

היה מקום לתרץ את הקושיא מקורת מבוי בכך שדין מבוי הוא מדרבנן ורק בו הקלו אבל לא בדאורייתא, אלא שעל זה מקשה התשב"ץ שלא מצינו בשום מקום שמקילים בדרבנן בדבר שאפשר לשערו ולידעו ורק בספיקא דרבנן אזלינן לקולא, מה שאין כן בדבר שאפשר לידעו, ואדרבה, חז"ל הזהירו שלא לזלזל ולהקל בשיעוריהם.

אומנם, למרות הדברים הללו, יש, אולי מקום מסברא להסביר שיטה זו, שנאמר שחכמים ראו שאי אפשר לעולם להגיע לדיוק אמיתי ולכן תקנו לסמוך על הכללים המקורבים שנתנו. לתקנה זו היה תוקף רק בדינים מדרבנן כמו בהרבה מקומות בש"ס- "הם אמרו והם אמרו", אבל לא היה לה כוח ולא פעלה ביחס לשיעורי תורה.

התשב"ץ הוסיף והקשה על שיטה זו מגמרא מפורשת, שמצינו שחז"ל הלכו עפ"י עיקריהם לקולא ובדאוריתא, למשל, בסוכה העשויה ככבשן ( סוכה ח ע"א).

דברים אלה דוחים כמה נסיונות תירוץ ליישב אי אלו סוגיות קשות מתוך שאינן תואמות את כללי החשבון. משום כך דחוקים דברי בעל התוספות יו"ט שניסה לתרץ את משנת עמוד עגול (אהלות פרק י"ב משנה ז) שחז"ל חשבו את π לפי ערכו האמיתי (מלבד מה שדבריו אינם מתרצים את הקושיא. ) הזה נדחית גם דברי התוספות יו"ט בקורת מבוי שרצה לומר שהואיל והיא דרבנן הקלו בה (וכבר התפלפל הרש"ש שם אם קורת מבוי היא באמת מדרבנן או לא)

דבר זה מצטרף עם כל הקושיות שיש על פירוש ר' פתחיה בשם הרמב"ם בעניין כורת (חידושי הרמבם לתלמוד, עמ' ב) שאביי לא נקט 53/5 אלא יותר בגלל הדיוק המתמטי 

עניין הגינה והקרקף (עירובין פרק ב משנה ה) שבו החשיבו חכמים את 2√ כגדול מ 1.4 וקבעו כ 2√*50=702/3 אעפ"י ש: 1.4*50=70 , עלול להפריע לשתי השיטות הנזכרות, שהרי לשתיהן לא סטו חז"ל מכלליהם. (אם לא שנאמר שחז"ל לא שינו מהכללים שבידם רק לעניין π ולא לענין 2√ שמכלל זה כן שאז יקשה מדין חלון עגול (עירובין ע"ו) וסוכה העשויה ככבשן שבהם סמכו על "אמתא ותרי חומשי" לקולא, וגם בדאוריתא - סוכה)

התשב"ץ דן בבעיה זו באריכות ודבריו אינם בהירים די הצורך. נראה מדבריו שכונתו לומר ששם למדנו מגזרת הכתוב "טול חמישים וסבב חמישים" (כך למדו שם בגמרא מדברי התורה - "ורחב חמישים בחמישים") שעלינו למצוא את 5000√ ולא להתייחס לדברים כאל אלכסון רגיל של ריבוע שאורך צלעו 50 אמה. לכן אין אנו קושרים במקרה זה לכלל: 2√=1.4 ואנו רשאים לדייק ב 5000√ כרצונינו, על כן הגענו לערך 702/3.

בסוגיית חלון עגול (עירובין ע"ו) שעליו נתנה הגמרא את הערך "שיבסר נכי חומשי" ושעליה כתב המאירי שיש לדייק לפי השיעור האמיתי ולא לסמוך על שיעורי הגמרא אלא ללכת לפי החשבון האמיתי שיתן תוצאה גדולה יותר. באותו עניין עצמו התלבט בעל "משנה-ברורה" ( ב"שער הציון" שלו סימן שע"ב סעיף-קטן י"ח) אם יש להחמיר יותר משיעור הגמרא כפי האמת, או לא, או בצורה מפשטת יותר, איזה דעה מההצעות הנ"ל היא הצודקת:

"ושיעור היקף עיגולו (של החלון) הוא ששה עשר טפחים ו ד' חומשי טפח דכשיעור זה יש השיעור של ד' טפחים על ד' טפחים מרובעים....ואף דבאמת יש מעט יותר, ונמצא לפי זה העיגול צ"ל יותר (מאשר לפי החשבון האמור בגמרא ע"ש) ובפרט לפי מה שכתב הרמב"ם בעירובין פרק א דמה שאמרו כל שיש בהיקפו ג' טפחים הוא גם-כן שלא בדקדוק האמת, נלענ"ד דאין לדקדק בזה יותר דסמכו חכמים על אלו השיעורים על עניינים שבתורה מפני שקשה לצמצם העודף. ואולי היה מקובל להם מסיני שיש לסמוך על השיעורים האלו אף בשיעורי תורה. ואיך שיהיה במילתא דרבנן בודאי יש לסמוך על השיעורים אלו, וכמעט כן משמע מהרמב"ם עי"ש"

המשנה ברורה מחליט שגם אם נאמר שלחז"ל לא היתה קבלה מסיני לסמוך על כלליהם, אפשר בדרבנן לסמוך עליהם. (ובמקומות שבהם נתנו שיעורים מקורבים עפ"י כלליהם לקולא ובדאוריתא. כגון סוכה העשויה ככבשן, אז צריך לומר , שנצטרך להחמיר, וכמו שכתב המאירי גם על הלכות דרבנן)

אפשר שכונת ה"משנה-ברורה" כזה היא מכיון שעומד לפנינו ספק, כאיזו דעה ההלכה, ולמעשה - האם יש להחמיר יותר משיעורי כמים או לא, עלינו ללכת לפי הכלל הרגיל בכל הספקות -

"ספיקא דאורייתא- לחומרא וספיקא דרבנן-לקולא"

וכשהמדובר בדין דרבנן עלינו להקל ולסמוך על שיעורי חכמים.

5.שתי סתירות מפורשות בין התלמוד והמתמטיקה

התוספות בעירובין ( י"ד ע"א ד"ה והאיכא) תמהו על שני מקומות בש"ס שמהם מוכח שהגמרא תפסה שבמציאות π=3. וכמעט שלא נמצא להם שום ישוב המניח את הדעת. קושיות אלו קשות לכל השיטות דלעיל. הגמרא שם דנה בקורת מבוי עגולה ובכלל "כל שיש בהיקפו שלושה טפחים יש בו רוחב טפח" ושואלת "מנא הני מילי?" והיא משיבה: "אמר ר' יוחנן: דאמר קרא: ויעש את הים מוצק עשר באמה משפתו עד שפתו, וקו שלושים באמה יסוב אותו סביב"( מלכים א פרק ז פסוק כ"ג)

על זה שואלת הגמרא: "והאיכא שפתו" כלומר, הקוטר, עשר אמות, מפורש בפסוק שהיה מגואי, מבפנים- "משפתו עד שפתו" ולא כלל את שפתו, אבל ההיקף של 30 אמה, לפי מה שמשמע לתלמוד, היה מאבראי וכלל גם את השפה, אם כן, כל שיש בהיקפו שלושה טפחים יש ברוחבו יותר מטפח. ומתרצת הגמרא: "אמר רב פפא: שפתו שפת פרח שושן היתה.." וא"כ חשבון זה דק והתנא לא דייק במשהו של שפת פרח שושן. הגמרא אינה מרפה ושואלת: "והאיכא משהו" והיה לתנא לדייק באותו משהו. ומתרצת הגמרא: "כי קחשיב - מגואי קחשיב" כלומר, שגם קוטר וגם ההיקף נאמרו מגואי ואם כן, כל שיש בהיקפו ג' טפחים יש בו רוחב טפח בדיוק.

מהדקדוק של הגמרא במשהו שנותר משמע שהחשבון של π=3 מדויק ומצומצם, ואפילו נאמר שיש כאן גזרת הכתוב או הלכה למשה מסיני שצריך להניח את החשבון האמיתי ולחשב בקירוב של π=3 בכל ענין, הרי יקשה על ים של שלמה עצמו, שמדקדוקי הגמרא משמע שסברה שקירוב זה הוא מדוייק גם במציאות.

קושיא זו תקשה אף לגירסת הב"ח בסוגיתינו שגרס שעל השאלה: "והאיכא שפתו" ענתה הגמרא:

"כי קחשיב מגואי קא חשיב, ואי בעית אימא, שפתו שפת פרח שושן היתה ואיכא משהו"

לפי גירסה זו, נשארת הגמרא למסקנא, בדעה שהמשנה לא דיקא, כי במציאות, כל שיש בהיקפו שלושה טפחים יש בו יותר מטפח ברוחבו, כי לפי 'האי בעית אימא' היה היקפו של הים מבחוץ 30 אמה ומבפנים, בלי השפה הדקה- 10 אמות. משמע מכאן שבמציאות π<3 אלא שבגלל ההבדל הקטן לא דייקה המשנה (ולחומרא) ונקטה π=3: לגירסת רבינו חננאל, תהיה קושית התוספות חמורה עוד יותר שלפיו, כתוב בקרא ש π<3 ובאמת π>3.

הגמרא במסכת בבא-בתרא (י"ד ע"ב) מסיקה שבארון שבקודש הקודשים היה מקום של שני טפחים כדי להכניס בו את ספר התורה שכתבו משה, כמו שכתוב (דברים פרק ל"א פסוקים כ"ה-כ"ו):

"ויהי ככלות משה לכתוב את דברי התורה הזאת על ספר עד תמם. ויצו משה את הלויים נושאי ארון ברית ה' לאמור: לקח את ספר התורה הז ושמתם אותו מצד ארון ברית ה' א-היכם"

לפי דעה זו, "מצד ארון ברית ה" כונתו, בתוך הארון ובצידו. חכמינו היו מקובלים שספר התורה שעשה משה היה בהיקפו שישה טפחים ונגלל לאמצעיתו, כלומר, שהיה מורכב משני עיגולים שהיקפו של כל אחד מהם 3 טפחים וקוטרו טפח לפי: π=3 וביחד שני טפחים.

על זה מקשה הגמרא:

בתרי פושכי היכי יתיב?

מכיון שהספר עצמו רחב שני טפחים, לא ייתכן שיכנס ויצא ברוח של שני טפחים שהרי צריך לשייר מקום לרוחא דביני ביני" כדי שאפשר יהיה להוציאו ולהכניסו צריך שיהא הרוח גדול קצת מהספר עצמו (קושיא זו חוזרת פעמים שם)

והרי לפי החשבון האמיתי -  π>3 אין קושיית הגמרא קושיא, שהרי כאן מדובר, לא בהלכה, איך לנהוג, אלא למעשה - איך היה ספר התורה בתוך הארון, ואם-כן, בהיקף 3 טפחים הרי הקוטר הוא קצת פחות מטפח, בערך 21/22 מטפח וסכום שני הקטרים הוא 42/22 בערך, שהם 21/11 , דהיינו שני טפחים חסר 1/11 ויש מקום לרוחא דביני ביני'.

וכך היא לשון התוספות:

"והאיכא משהו, משמע שהחשבון מצומצם וכן בפרק קמא דבבא-בתרא גבי שני טפחים שנשתיירו בארון ששם ס"ת מונח שהיא בהיקפה שישה טפחים, ופריך, כיון דלאמצעיתו נגלל - נפיש ליה משני טפחים וכן בתר הכי דמשני בספר עזרה לתחילתו הוא נגלל ופריך, אכתי תרי בתרי היכי יתיב. משמע דמצומצם לגמר. וקשיא שאין החשבון מדוקדק לפי חכמי המידות"

לקושיות אלו לא ניתן ישוב במפרשים, אולם יש לציין כי נאמר עליהן ישוב שבמחשבה המקריב את הדברים לתחום הקבלה, ע"י מתתיהו הכהן מונק (במאמרו "שלש בעיות הנדסיות בתנ"ך ובתלמוד")

הוא יוצא מתוך הדעה (ראה לעיל סעיף 3) שמה שלא דייקו חז"ל בערכו האמיתי של  π, זה משום שלא היו צריכים לדייק בו כלל כי ניתן למשה בסיני שאין לנו לדקדק בו יותר מ 3.

אף הוא דורש קרי וכתיב בפסוק של ים שעשה שלמה, שאחרי שאמר "עגול סביב" הוסיף ואמר "וקו שלושים באמה יסוב אותו סביב" שהוא יתור ואריכות בלשון, שהרי יכול היה לומר עגול סביב שלושים באמה.

וכדומה, ומה הטעם שהוסיף "וקו...יסוב אותו סביב"? על כך עונה מונק שזאת הוסיף הנביא מחמת המילה "וקו" שיש בה קרי וכתיב ואותם רצה ללמד, כתיב "קוה" וקרין "קו". הרמז בזה הוא בגימטריה של שתי מילים אלו. הערך של קוה בגימטריה הוא 111 והגימטריה של קו היא 106. היקפו של הים , לפי חשבוננו היה צריך להיות 10π. אם ניקח כ π את הערך המקורב 333/106 שהוא קרוב יותר מן הערך המקובל 22/7, הרי צריך שהקו של ים הנחושת להיות 3330/106 שהוא הערך שיתקבל מחילוק הערך שנתן הנביא בפירוש - שלושים אמה - ביחס שבין שני הערכים שנתן ברמז - בגימטריא:

30=106/111=3330/106

מן הדברים הללו מגיע מונק לומר כי המספר שלש יש בו קדושה מיוחדת שעניינה הוא רק בקבלה, "למי שבא בסוד ה'" כלשונו. הוא מפנה אותנו לרמזים שבאו בילקוט-שמעוני (על מלכים א. רמז קפ"ה) ביחס לים הנחושת , כי העשר אמות מרמזים על עשרת הדברות, עשרה מאורות, עשר ספירות ו - 30 האמות שבהיקפו הם כנגד שלושים ימי החודש.

הוא משתמש באחד היסודות הידועים בספרות המחשבה שכנגד כל דבר ודבר בעולם החומר יש לו משפיע ומאציל עליו ובכך מאפשר את קיומו. מתוך אלה קובע הוא שהיחס בעולם העליון בין מה שמסמל שם את קוטר העיגול לבין היקפו הוא 3 בדיוק, אותו מספר שיש בו בקדושה ושהעולם התחתון לא יכול להגיע אליו.

בית-המקדש הוא המקום שבו היתה שרויה השכינה וקרו בו תדיר עשרה ניסים, שם היה היחס במציאות שלש בדיוק - בית המקדש הוא מעין "שגרירות" של העולם הרוחני בעולם הגשמי. לכן, גם ים הנחושת וגם ספר התורה שבארון הברית, היה היקפם גדול מקוטרם בדיוק פי שלוש.

(ואלי יש להוסיף לזה שבגמרא בבא-בתרא שם אמרו שספר-תורה שעשה משה היה היקפו שווה לאורכו- שישה טפחים, רק מעטים הצליחו לעשות כמותו. עתה נאמר שספר התורה שעשה משה, הוד של קדושת המשכן והמקדש חפץ עליו ורק מעטים הצליחו להגיע למדרגה זו, ואין כאן עניין של בעיה טכנית בלבד)

לכן צריכים אנו, בקיום המצוות, שנועדו, לפי הקבלה, לתקן את עולם החומר, לנהוג על פי המידות של העולם העליון - "כל שיש בהיקפו שלושה טפחים - יש בו רוחב טפח"

עוד זאת מוסיף הוא ודורש ע"פ החידוד המשוה את הערך המספרי של קו ו קוה הוא מביא שני פסוקים העוסקים בגאולה העתידה שיש בהם קרי וכתיב זה:

"ויצא עוד קו (כתיב קוה) המידה" (ירמיהו פרק ל"א פסוק ל"ח)

"וקו (כתיב קוה) ינטה על ירושלים" (זכריה פרק א פסוק ט"ז)

גם בפסוקים אלה, יש לדרוש שכשם שבים הנחושת השתנתה המידה הגשמית למידה הרוחנית, כך שישתנו לעתיד לבוא כל המידות, כמידות הרוחניות הגבוהות ומלאה הארץ דעה את ה'.

(שיטתו ההלכתית של מונק, לקמן פרק ח ותירוץ נוסף לבעיה שם, סעיף 1 )

תירוצים שונים נאמרו על השאלה איך נוכל לקבל את הכלל של המשנה π=3 (הובאו בפרק זה ובפרקים קודמים) מעניין תירוצו התמוה של בעל "תפארת ישראל" שכתב (על פרק א משנה ה) בשגגה שיצאה מתחת יד השליט:

"ואין החשבון מדוקדק דהיקף ג' טפחים יש ברוחבו טפח ושביעית טפח ולחומרא לא דק"

הוא הפך את דברי הרמב"ם בפירושו למשנתינו שכתב π=31/7. מכאן החליט בעל ה"תפארת ישראל" שבהיקף 3 יש קוטר של 11/7 והתנא לא דק לחומרא. בעוד שלפי האמת לא דק לקולא. (לדברי התפארת ישראל לא מובנת גם קושית התוס' על ספר התורה של עזרה, שאם במציאות גדול הקוטר משיעורי חכמים, ודאי שאין הספר נכנס בשני טפחים)

לפי גירסת הר"ח שהבאתי לעיל בסעיף זה, שהמקרא לא דקדק בשיעורו אפילו אם אי דיוק זה גורם שכל שיש בהיקפו שלושה - יש בקוטרו יותר מאחד, תקשה , לכאורה, קושית התוספות יותר , אלא שנוכל לומר שמכיון שלפי גירסא זו אין החשבון מצומצם, נוכל לתלות בפסוק אי-דיוק גדול יותר. את הסיבה לכך שהנביא לא הודיע את ההיקף המדויק אלא אמר "וקו שלושים באמה יסוב אותו" בשעה שהוא כמעט 31.5 אמה ובפרט לפי גרסת רבנו חננאל שהקוטר היה גדול מ 10 אמות, תולה בעל "מראה-הפנים" על הירושלמי (עירובין פרק א הלכה ה) שבכך שהנביא לא עשה את דבריו פרוטרוט ונתן חשבון כללי במידות שלמות כמו שמצינו בכמה מקומות , כגון "שש מאות אלף רגלי" שאינו מדויק שבמקום אחר נמנו "שש מאות אלף ושלושת אלפים.." ועוד כיוצא בו.

(*בתשובה למאמר "שלש בעיות הנדסיות" של מונק, הראה המשיב אסא כשר, עוד מקום שבו השתמשו חז"ל, לא להלכה, אלא לשם קביעת עובדה בקירוב π=3 (שגם מדרשיו של מונק אינם תופסים בו) ובעניינים אסטרונומיים שאין לנקוט בהם בשיעורים מקורבים, ובפרט בהפרש כה גדול יחסית (כ 4%) הוא הביא קטע מברייתא דשמואל הקטן (פרק א) בזו הלשון:

"הרקיע עשוי כקובה...עגולה ככבשן, שנאמר: עושה עש כימה וכסיל וחדרי תימן....סביב שמונה עשר ברוחב שישה" )